Learning maximum likelihood tree structure with the Chow-Liu algorithm
Taken from coursework for ECE 7751: Graphical Models in Machine Learning, taught by Faramarz Fekri at Georgia Tech, Spring 2023
Write a function ChowLiu(X) -> A where X is a D by N data matrix containing a multivariate data point on each column that returns a Chow-Liu maximum likelihood tree for X.
The tree structure is to be returned in the sparse matrix A.
The file ChowLiuData.mat contains a data matrix for 10 variables.
Use your function to find the maximum-likelihood Chow-Liu tree, and draw a picture of the resulting DAG with edges oriented away from variable 1.
Solution
from scipy.io import loadmat
data = loadmat('ChowLiuData.mat')['X'].T - 1
print(data.shape)
data
(1000, 10)
array([[0, 1, 1, ..., 2, 1, 0],
[1, 1, 1, ..., 0, 2, 0],
[0, 0, 1, ..., 2, 1, 1],
...,
[1, 1, 1, ..., 0, 2, 0],
[1, 1, 0, ..., 0, 0, 0],
[1, 0, 1, ..., 2, 1, 0]], dtype=uint8)
The Chow-Liu algorithm simply computes the mutual information $I(X_i,X_j)$ between each pair of variables and constructs a maximum spanning tree where the edge weights are the mutual information.
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
def chow_liu(X):
M, N = X.shape
K = X.max() + 1 # num discrete values each X can take
# compute empirical p(x_i, x_j)
p_pair = np.zeros((N, K, N, K))
# and empirical p(x_i)
p_single = np.zeros((N, K))
for row in X:
for i in range(N):
p_single[i, row[i]] += 1
for j in range(i, N):
p_pair[i, row[i], j, row[j]] += 1
if i != j:
p_pair[j, row[j], i, row[i]] += 1
p_pair /= M
p_single /= M
assert np.allclose(p_pair.sum(axis=(1, 3)), 1)
assert p_single.shape == (N, K)
assert np.allclose(p_single.sum(axis=1), 1)
# compute all I_ij = I(X_i, X_j)
with np.errstate(divide='ignore', invalid='ignore'):
logterm = (np.log(p_pair) \
- np.log(p_single[..., np.newaxis, np.newaxis]) \
- np.log(p_single))
# set these to constants, will be nullified assuming they come from
# instances when p_pair=0
assert np.all(p_pair[np.isnan(logterm)] == 0)
logterm[np.isnan(logterm)] = 1 # from log0 - log0
assert np.all(p_pair[np.isinf(logterm)] == 0)
logterm[np.isinf(logterm)] = 1 # from log0 - ...
I = (p_pair * logterm).sum(axis=(1, 3))
assert I.shape == (N, N)
# compute max spanning tree
G = nx.Graph()
G.add_nodes_from(range(1,N+1))
for i in range(1, N+1):
for j in range(i, N+1):
G.add_edge(i, j, weight=I[i-1, j-1])
T = nx.maximum_spanning_tree(G)
# get directions from breadth-first search
A = nx.bfs_tree(T, 1)
return A
A = chow_liu(data)
d = nx.draw_planar(A, with_labels=True)
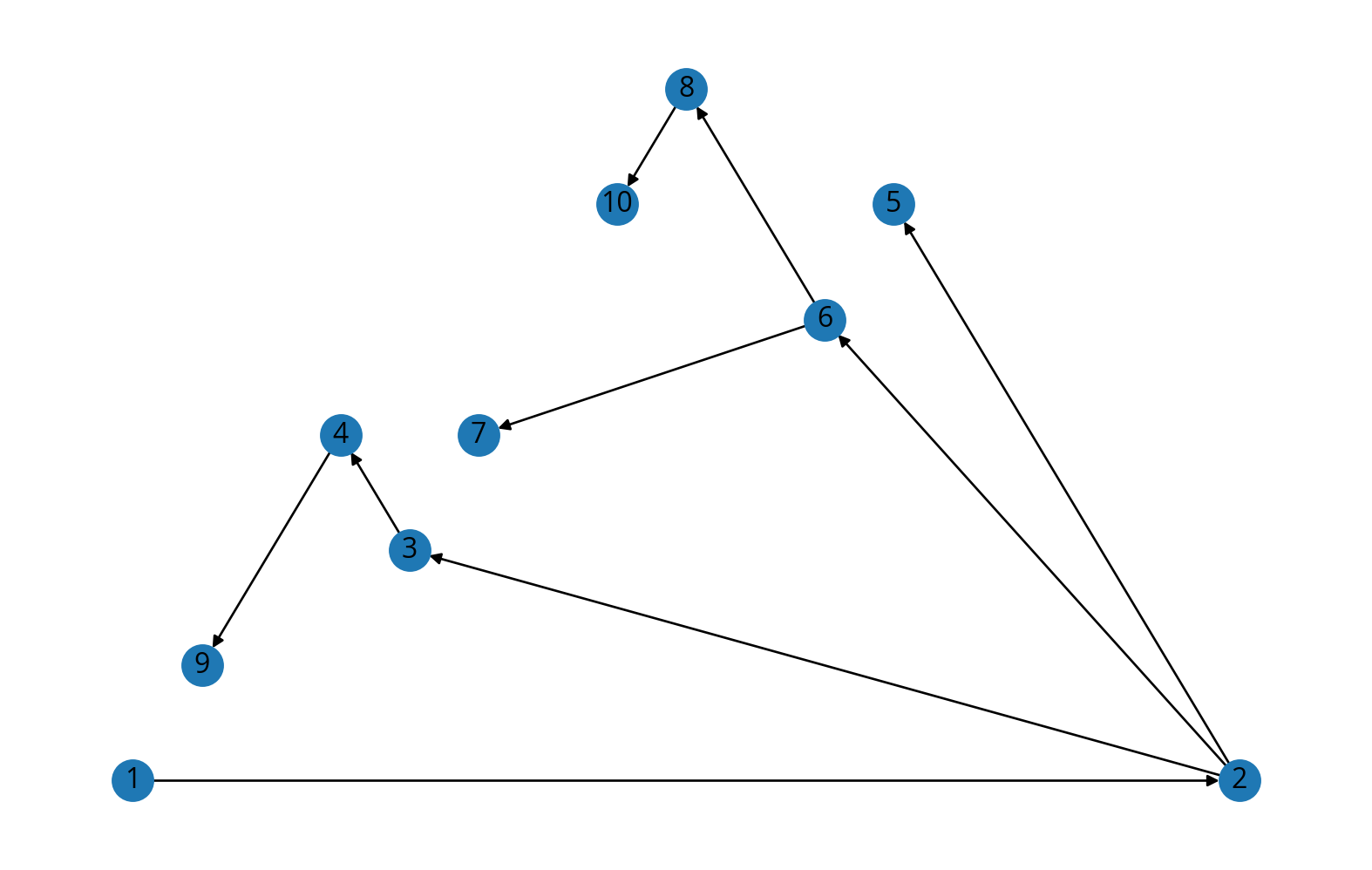
The directions are coincidental from the breadth-first search—the result is an undirected tree (Markov random field).
Kyle Johnsen
PhD Candidate, Biomedical Engineering
My research interests include applying principles from the brain to improve machine learning.